AI/혼공학습단9기_DL&ML

[혼공머신] 5주차 과제 - 비지도 학습

moviewine 2023. 2. 1. 20:02

1. Contents

1) 군집 알고리즘(Clustering)

  • Unsupervised Learning(비지도학습)은 머신러닝의 한 종류로 훈련 데이터에 타겟이 없음. 따라서 외부 도움 없이 스스로 학습해야 함. 대표적인 비지도학습은 Clustering(군집), Dimension Reduction(차원 축소: PCA, tSNE 등)이 있음.
    • Clustering(군집)은 비슷한 샘플끼리 하나의 그룹으로 모으는 대표적인 비지도 학습임. 군집 알고리즘으로 모은 샘플 그룹을 Cluster라고 부름.
  • Histogram(히스토그램: hist())은 구간별로 값이 발생한 빈도를 그래프로 표시한 것. 보통 x축이 값의 구간이고 y축은 발생 빈도임.


2) K-MEANS

  • K-Means(K-평균) 알고리즘은 처음에 랜덤하게 클러스터 중심을 정하고 클러스터를 만들며, 그 이후 클러스터 중심을 이동하고 다시 클러스터를 만드는 식을 반복하여 최적의 클러스터를 구성하는 알고리즘.
    • n_clusters에는 클러스터 개수를 지정(기본값: 8)
    • 처음에는 랜덤하게 centroid를 초기화 하기 때문에 여러 번 반복하여 이너셔를 기준으로 가장 좋은 결과를 선택(n_init: 반복 횟수, 기본값: 10)
    • max_iter는 K-Means 알고리즘의 한 번 실행에서 최적의 센트로이드를 찾기 위해 반복할 수 있는 최대 횟수(기본값: 200)
  • Centroid 또는 Center of Cluster(클러스터 중심)은 K-Means 알고리즘이 만든 클러스터에 속한 샘플의 특성 평균값. 가장 가까운 클러스터 중심을 샘플의 또 다른 특성으로 사용하거나 새로운 샘플에 대한 예측으로 활용할 수 있음.
  • Elbow(엘보우) 방법은 최적의 클러스터 개수를 정하는 방법 중 하나임.
    • Inertia는 클러스터 중심과 샘플 사이 거리의 제곱 합임.
    • 클러스터 개수에 따라 Inertia 감소가 꺾이는 지점이 적절한 클러스터 개수 K가 될 수 있음(그래프 모양을 따라 엘보우 방식이라 부름)


3) 주성분 분석(Principle Component Analysis)

  • Dimension Reduction(차원 축소)는 원본 데이터의 특성ㅇ르 적은 수의 새로운 특성으로 변환하는 비지도 학습의 한 종류로서, 저장 공간을 줄이고 시각화 하기 쉬움. 또한 다른 알고르짐의 성능을 높일 수 있음.
  • Pricipal Component Analysis(PCA: 주성분 분석)은 차원 축소 알고리즘의 하나로 데이터에서 가장 분산이 큰 방향(주성분)을 찾는 방법. 원본 데이터를 주성분에 투영하여 새로운 특성을 만들 수 있으며, 일반적으로 주성분은 원본 데이터의 특성 개수보다 작음.
  • Explained Variance(설명 가능한 분산)은 주성분 분석에서 주성분이 얼마나 원본 데이터의 분산을 잘 나타내는지 기록한 것으로서 scikit-learn의 PCA 클래스는 주성분 개수나 설명된 분산의 비율을 지정하여 주성분 분석을 수행할 수 있음.
    • PCA에서 n_components를 통해 주성분의 개수를 지정(기본값: None - 샘플 수와 특성 수 중 작은 값 사용)
    • random_state에는 numpy random seed 값을 지정할 수 있음.
    • components_ 속성에는 train set에서 찾은 주성분이 저장
    • explained_variance_ 속성에는 설명된 분산이 저장되고, explained_variance_ratio_에는 설명된 분산의 비율이 저장
    • inverse_transform() 메서드는 transform() 메서드로 차원을 축소시킨 데이터를 다시 원본 차원으로 복원



2. K-Means 알고리즘 작동방식 설명하기

  • K-Means 군집 알고리즘: 각 군집(cluster)의 평균값(cluster center or centroid)을 자동으로 찾아 분류해주는 알고리즘
  • K-Means 알고리즘 작동 방식
    1. 무작위로 k개의 클러스터 중심을 정함ㅣ
    2. 각 샘플에서 가장 각까운 클러스터 중심을 찾아 해당 클러스터 샘플로 지정
    3. 클러스터에 속한 샘플의 평균값으로 클러스터 중심을 변경
    4. 클러스터 중심에 변화가 없을 때까지 2번 과정에서 부터 다시 반복
  • 즉, K-Means 알고리즘은 처음에는 random하게 클러스터 중심을 선택하고 점차 가까운 샘플의 중심으로 이동하는 알고리즘임.

 

  • K-Means 클래스 실습
    • KMeans 모델을 학습 시키기 위한 데이터를 wget을 통해 불러오고, 넘파이 배열(npy)로 저장합니다.

Data Preparation

 

  • Sample에 저장되는 npy파일은 3차원 배열로서 (샘플 개수, 너비, 높이)입니다. 
  • 이것은 KMeans 모델 학습을 위해 2차원 배열(샘플 개수, 너비 * 높이)로 reshape시킵니다.
  • Scikit-learn의 KMeans알고리즘을 sklearn.cluster로 부터 불러들여 오며, 매개변수로서 n_clusters 를 3으로 지정합니다.
  • Kmeans는 비지도 학습이므로 fit()메서드에서 target(타켓)을 사용하지 않습니다.
  • Clustering 된 결과는 KMeans 클래스 객체의 labels_ 속성에 저장되므로, "km.labels_"로서 확인할 수 있습니다.

KMeans model & fit

 

  • 각 cluster 가 어떤 이미지를 나타냈는지 그림으로 출력하기 위해 "draw_fruits()"라는 함수를 정의 후 사용합니다. "draw_fruits()"라는 함수는 subplot을 이용해 이미지를 plot 해주도록 만든 함수입니다. Clustering된 결과가 "km.labels_"에 저장되어 있으므로, label을 지정할 때마다 (draw_fruits(fruits[km.labels_==0]) 형태로 label에 해당되는 샘플의 이미지를 확인할 수 있습니다.

Clustering & Image Show -1
Clustering & Image Show -2

 

  • KMeans 클래스가 최종적으로 찾은 cluster의 중심은 "cluster_centers_"속성에 저장됩니다. 이것은 2차원 이미지의 중심점이므로, 2차원 배열로 reshape해야 확인할 수 있습니다.
  • KMeans의 transform() 메서드를 사용하면 샘플에서 클러스터 중심까지의 거리를 수치로 변환해 확인할 수 있습니다. transform()메서드가 있다는 것은 StandardScaler() 클래스와 같이 특성값을 변환하는 도구로 사용할 수 있다는 의미입니다.
  • transform() 메서드도 fit()와 마찬가지로 2차원 배열을 필요로 합니다.
  • Cluster 중심을 옮기며 최적의 중심을 찾는데 반복하는 횟수는 "n_iter_"속성에 저장됩니다.

 

  • 최적의 k 찾기 위한 방법은 앞서 언급된 transform() 메서드를 통해 계산되는 거리를 통해 이루어지는데, 이 거리 제곱의 합을 Inertia(이너셔)라고 합니다. 일반적으로 cluster개수가 늘어나면 클러스터 개개의 크기가 줄어들기 때문에 inertia도 줄어듭니다.
  • Elbow(엘보우) 방법은 cluster 개수를 늘려가면서 inertia 변화를 관찰하며 최적의 cluster 개수를 찾는 방법이며, cluster vs inertia 그래프에서 감소 추이가 꺽이는 위치를 최적의 클러스터 수로 보고 있습니다.

Centroid 분석
최적의 클러스터 개수(K)를 찾기 위한 Elbow 방법 및 Inertia



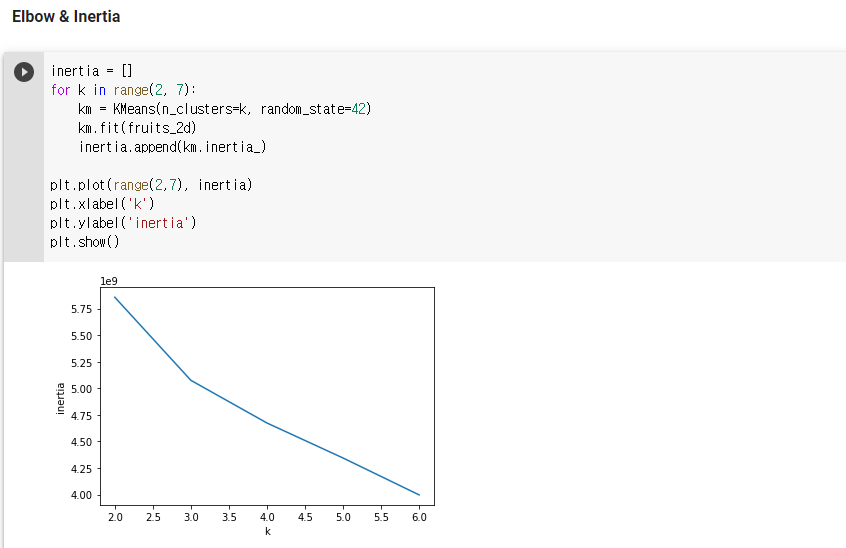
3. 주성분 분석 문제

1) 특성이 20개인 대량의 데이터 셋에서 찾을 수 있는 주성분 개수?
: 특성 개수 이하로 주성분을 찾을 수 있으므로 20개 입니다. 그러나 보통 주성분 분석을 사용한다면 그 보다 적은 주성분을 찾도록 설정할 것입니다.

2) 샘플 개수가 1,000개이고 특성 개수는 100개인 데이터셋 (1000, 100)에서 scikit-learn PCA 클래스를 사용해 10개의 주성분을 찾아 변환할 경우 크기는?
: 100개의 특성에서 10개의 주성분을 찾아 변환하면 (1000, 10)입니다. 샘플의 개수는 그대로이고 특성 개수만 바뀌기 때문입니다.

3) 2번 문제에서 설명된 분산이 가장 큰 주성분은 몇 번째인가?
: 주성분 분석은 가장 분산이 큰 방향부터 순서대로 찾기 때문에 설명된 분산이 가장 큰 주성분은 첫 번째 입니다.