-
[혼공머신] 2주차 과제 - 회귀모델AI/혼공학습단9기_DL&ML 2023. 1. 12. 06:51
1. 2주차 Contents
- 회귀(Regression): 타겟값(임의의 수치)를 예측하는 기법
- KNeighborsRegressor(): 가장 가까운 이웃 샘플을 찾고 이 샘플들의 타겟값을 평균하여 예측. n_nighbors 매개변수로 이웃의 개수를 지정하며 기본값은 5.
- mean_absolute_error(): 평균 절대값 오차. 첫 번째 매개변수는 타겟, 두 번째 매개변수는 예측값을 전달하며 비슷한 개념의 평균 제곱 오차(mean_squared_error())는 이에 제곱근을 을 씌운 개념임.
- reshape(): 배열의 크기를 바꾸는 메서드
- 결정계수(R2): 회귀문제 성능 측정도구. 1에 가까울 수록 성능이 좋은 모델
- 과대적합(Overfitting): 모델이 trainset에 너무 집착해 데이터에 내재된 거시적 패턴을 감지 못하는 경우. 보통 trainset 성능이 testset보다 훨씬 높을 때 발생.
- 과소적합(Underfitting): Overfitting의 반대. trainset과 testset 성능이 모두 동일하게 낮거나 testset성능이 오히려 높을 때 발생(복잡한 모델을 사용하거나 데이터 샘플을 늘려 재 학습 필요)
- 선형회귀(LinearRegression): 특성과 타깃 사이 관계를 잘 나타내는 선형방정식을 찾는 기법. 계수와 가중치를 저장함.
.coef_: 특성에 대한 계수를 포함한 배열.
.intercept_: 절편 저장되어 있음. fit_intercept 매개변수를 False로 지정하면 절편을 학습하지 않음.
- 모델 파라메터: LinearRegression이 찾는 가중치 처럼 머신러닝 모델이 특성에서 학습한 파라메터
- 다항회귀(Multi-Regression): 다항식을 사용하여 특성과 타겟 사이의 관계를 찾는 기법
- 다중회귀(Multiple Regression): 여러 개의 특성을 사용하는 회귀 모델
- 특성공학: 주어진 특성을 조합하여 새로운 특성을 만드는 작업
- 릿지(Redge Regression): 규제가 있는 선형 회귀 모델 중 하나(과대 적합 완화 효과). alpha 매개변수로 규제 강조 조절(기본값: 1). sover는 sag 또는 saga가 가장 우수한 성능을 보임.
- 라쏘(Lasso Regression): 규제가 있는 선형 회귀 모델 중 하나(계수 값을 0으로 만들 수 있는 좌표하강법)
- 하이퍼 파라메터(Hyper Parameter): 머신러닝 알고리즘이 학습하지 않는 파라메터로서 개발자가 직접 지정하는 변수.
- read_csv(): csv파일을 pandas data frame으로 변환하는 함수. 매개 변수 sep은 csv파일 구분자를 자정(기본값은 콤마), header는 data frame 열이름으로 사용할 csv파일 행번호, skiprows는 파일을 읽을 때 건너띌 행의 개수, nrows는 파일에서 읽을 행의 개수.
- PolynomialFeatures: 특성을 조합하여 새로운 특성 생성. degree는 최고 차수(기본값: 2), interaction_only는 특성간의 곱셈 항만 추가(거듭제곱 제외), include_bias는 절편을 위한 특성.
2. Ch.03(03-1) 2번 문제 출력 그래프 인증하기
1) 데이터 전처리
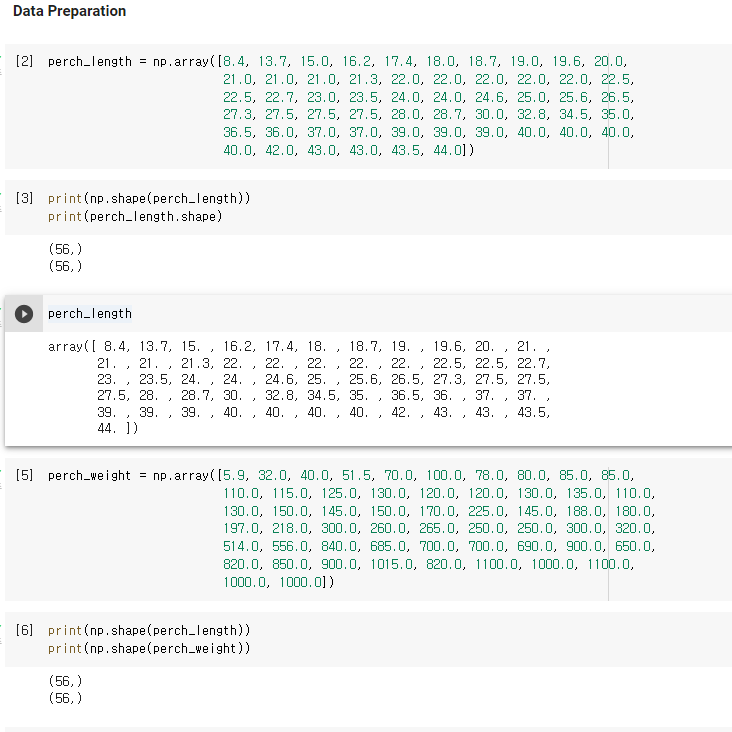
- 농어의 길이와 무게 데이터를 입력한 후, 데이터 수 및 shape을 검토 합니다.
- 입력한 데이터는 1차원 배열이며, 원소가 1개인 tuple 형태입니다.
- 학습을 위해서는 2차원 배열로 만들기 위해 reshape(-1, 1)을 해야 합니다(아래 추가 설명).
데이터 전처리 -1 - 앞서 1차원, 2차원 배열에 대해 언급이 되었는데, 좀 더 응용을 해 봅니다.
- 아래 test_array라는 1차원 배열을 원소 2개의 2차원 배열로 변경한 예를 볼 수 있습니다.
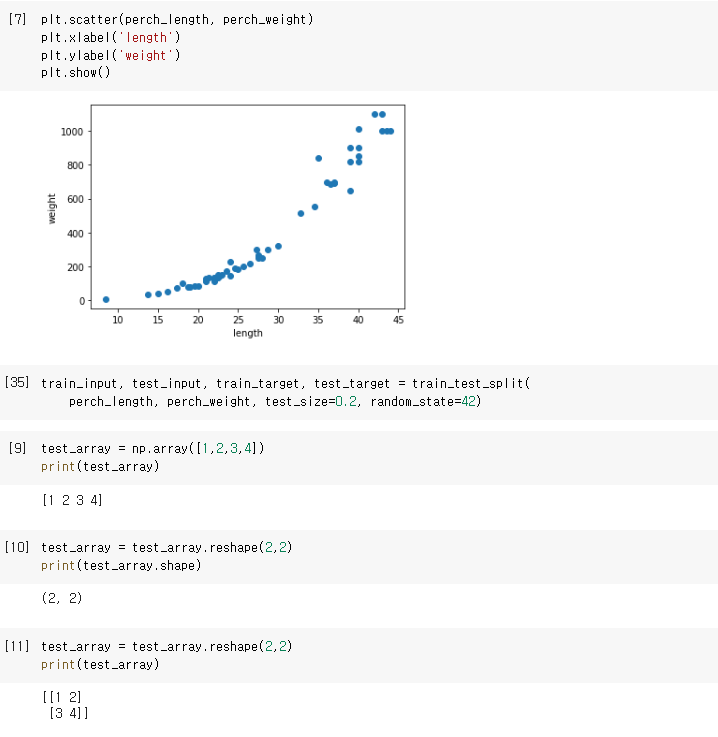
데이터 전처리 -2 - 선형 회귀(KNeighborsRegressor) 학습을 위해서는 복수의 원소를 갖는 1차원 배열 형태를 갖춰야 합니다.
- data.reshape(-1, 1) 함수를 이용하여 1차원 배열을 2차원으로 변경한 후, 데이터 전처리를 마칩니다.
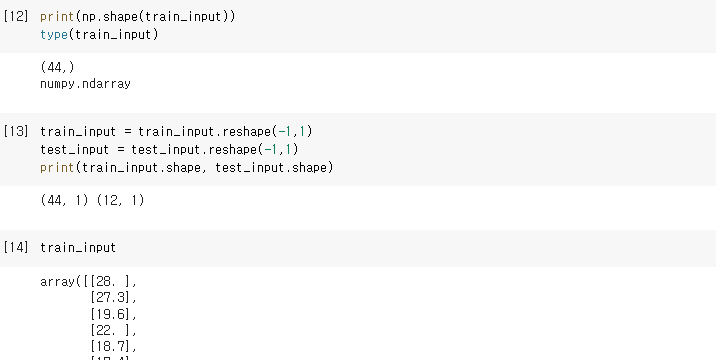
데이터 전처리 -3 2) 학습 및 추론
- KNeighborsRegressor() 선형 회귀 모델을 'knr'이란 변수로 선언한 후, fit을 통해 모델을 학습 시킵니다.
- 아래와 같이 농어 길이와 무게 데이터의 학습 결과(score)는 약 99.3%가 나왔습니다.
- test set data를 이용해 추론을 할 때는 model.predict(testset data)를 입력합니다.
아래 예시에서, knr.predict(test_input)입니다.
- 오차의 확인은 mean absolute error(mae)를 사용하였습니다.
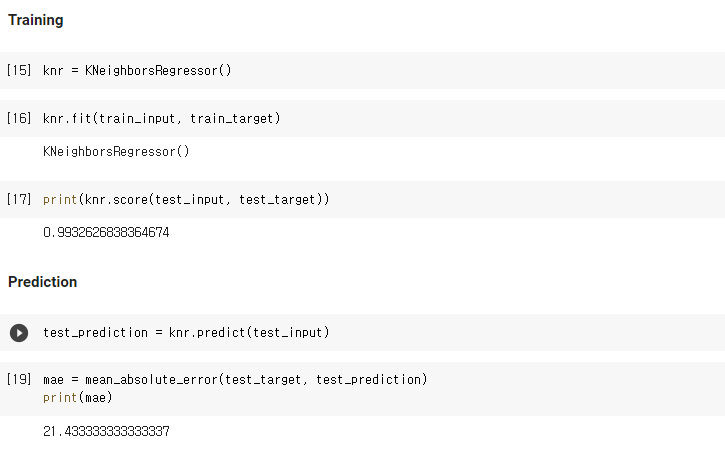
학습(training) 및 추론(inferencing) 3) 과대적합 / 과소적합 확인
- Train set 결과(score)와 Test set 결과를 비교하여, 과대/과소 적합 여부를 판단합니다.
- 아래 그림과 같이 train set이 test set의 score보다 높아 과대적합은 아님을 알 수 있습니다.

과대적합 / 과소적합 확인 4) 과제 미션
- 미션: n_neighbors를 변경(1, 5, 10)해 가며, 농어 길이에 따른 예측 결과 검토하기
- 결과: 아래 그래프에서 n_neighbors가 커질 수록(1 -> 5 -> 10), 이웃(주변 값)의 영향을 많이 받아 fitting이 더욱
부드러워 졌습니다.
실전에서는 목적에 따라 1개라도 값을 정확하게 예측 해야 할 경우는 n_neighbors를 작게, 정확도가 다소
떨어지더라도 전반적으로 일관된 예측을 원할 때는 n_neighbors를 크게 설정해야 할 것 같습니다.
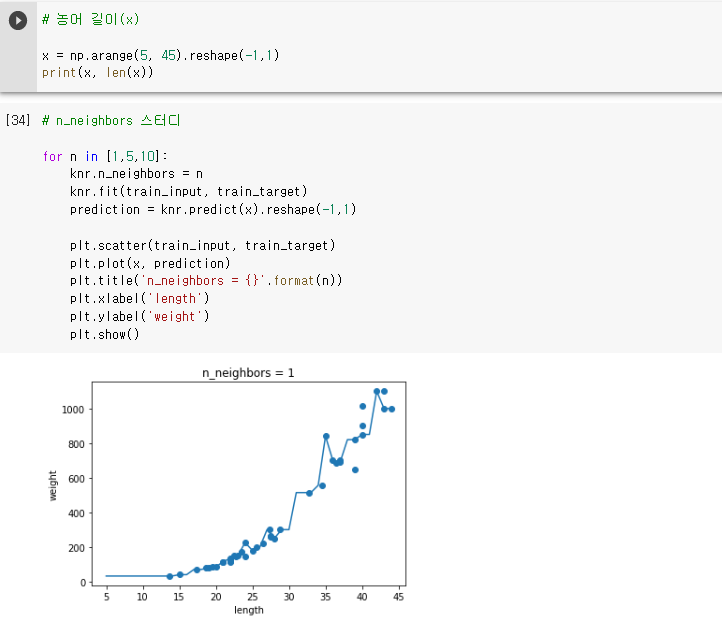

미션 결과 3. 모델 파라미터에 대해 설명하기
- LinearRegression이 찾는 가중치 처럼 머신러닝 모델이 특성에서 학습한 파라메터
- LinearRegression에서 coef_와 intercept_가 머신러닝 알고리즘이 찾는 모델 파라메터임.
- 최적의 모델 파라메터를 찾는 것이 머신러닝 알고리즘의 목표 => 모델 기반 학습
- "model.coef_" 와 "model.intercept_"로 확인 가능함.
'AI > 혼공학습단9기_DL&ML' 카테고리의 다른 글
[혼공머신] 5주차 과제 - 비지도 학습 (0) 2023.02.01 [혼공머신] 4주차 과제 - 트리 알고리즘 (0) 2023.01.26 [혼공머신] 3주차 과제 - 다양한 분류 알고리즘 (0) 2023.01.19 [혼공머신] 1주차 과제 - 데이터 전처리, 훈련/시험세트 (0) 2023.01.08 혼공학습단으로 시작하는 딥러닝 공부 !! (0) 2023.01.08